Dubins yolu - Dubins path
İçinde geometri, dönem Dubins yolu tipik olarak iki boyutlu iki noktayı birleştiren en kısa eğriyi ifade eder. Öklid düzlemi (yani x-y düzlem) üzerinde bir kısıtlama ile eğrilik yolun ilk ve son teğetler ve yolu giden aracın yalnızca ileriye gidebileceği varsayımı. Araç ters yönde de gidebiliyorsa, yol Reeds-Shepp eğrisini takip eder.[1]
1957'de Lester Eli Dubins (1920–2010) [2] analiz araçlarını kullanarak kanıtlandı [3] bu tür herhangi bir yol maksimum eğrilikten ve / veya düz çizgi parçalarından oluşacaktır. Diğer bir deyişle, en kısa yol, maksimum eğrilikteki dairesel yaylar ve düz çizgiler birleştirilerek yapılacaktır.
1974'te H.H Johnson, Dubins'in sonucunu başvurarak kanıtladı Pontryagin'in maksimum prensibi.[4] Özellikle, H.H Johnson, parça parça sürekli eğriliği sınırlayan ve minimum uzunluğa sahip olmak için başlangıç ve bitiş noktaları ve yönlerini öngören bir düzlem eğrisi için gerekli ve yeterli koşulları sundu. 1992'de aynı sonuç kullanılarak tekrar gösterildi Pontryagin'in maksimum prensibi.[5]
Dubins yolu yaygın olarak şu alanlarda kullanılır: robotik ve kontrol teorisi tekerlekli robotlar, uçaklar ve su altı araçları için yollar planlamanın bir yolu olarak. Basit geometrik var [6] ve analitik yöntemler [7] optimum yolu hesaplamak için.
Örneğin, tekerlekli bir robot durumunda, sistemler için basit bir kinematik araba modeli:
nerede arabanın konumu, rota, araba sabit bir hızda hareket ediyor ve dönüş hızı kontrolü Sınırlı. Bu durumda, maksimum dönüş hızı bir miktar minimuma karşılık gelir dönüş yarıçapı (ve eşdeğer olarak maksimum eğrilik). Öngörülen ilk ve son teğetler, başlangıç ve bitişe karşılık gelir başlıklar. Dubins'in yolu, tekerlekli robot modeli için mümkün olan iki yönlendirilmiş noktayı birleştiren en kısa yolu verir.
En uygun yol türü, arabalarla 'sağa dönüş (R)', 'sola dönüş (L)' veya 'düz (S)' sürüş benzetimi kullanılarak tanımlanabilir. En uygun yol her zaman altı türden en az biri olacaktır: RSR, RSL, LSR, LSL, RLR, LRL. Örneğin, verilen bazı ilk ve son konumlar ve teğetler için en uygun yolun 'RSR' türünde gösterildiğini düşünün. Daha sonra bu, bir sağa dönüş yayına (R) ve ardından düz bir çizgi segmentine (S) ve ardından başka bir sağa dönüş yayına (R) karşılık gelir. Bu sıradaki her parça boyunca uygun uzunluk için hareket etmek, bir başlangıç noktası A ile bir terminal noktası B'yi her son noktada istenen teğetlerle birleştiren ve verilen eğriliği aşmayan en kısa eğriyi oluşturacaktır.
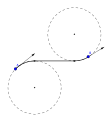
RSL Dubins yolu
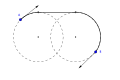
RSR Dubins yolu
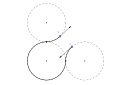
Bir LRL Dubins yolu
Dubins Aralık Problemi
Dubins aralığı problemi, Dubins yol probleminin temel bir varyantıdır; burada, başlangıç ve terminal noktalarında bir yön yönü aralığı belirtilmiştir. Yolun ilk ve son noktalardaki teğet yönü, belirtilen aralıklar içinde kalacak şekilde sınırlandırılmıştır. Bunu geometrik analiz kullanarak çözebiliriz.[8] veya Pontryagin'in minimum prensibini kullanarak.[9]
Referanslar
- ^ Kamışlar, J.A. ve L.A. Shepp, "Hem ileri hem de geri giden bir araba için en uygun yollar", Pacific J. Math., 145 (1990), s. 367–393.
- ^ "MEMORIAM'DA Lester Eli Dubins Matematik ve İstatistik Profesörü, Emeritus UC Berkeley 1920–2010". Kaliforniya Üniversitesi. Arşivlenen orijinal 15 Eylül 2011'de. Alındı 26 Mayıs 2012.
- ^ Dubins, L.E. (Temmuz 1957). "Ortalama Eğrilik Üzerinde Bir Kısıtlamayla ve Öngörülen Başlangıç ve Terminal Konumları ve Teğetleriyle Minimum Uzunluktaki Eğriler Üzerinde". Amerikan Matematik Dergisi. 79 (3): 497–516. doi:10.2307/2372560. JSTOR 2372560.
- ^ Johnson, H. H "Maksimum prensibinin düzlem eğrilerinin geometrisine uygulanması", Amerikan Matematik Derneği Bildirileri, 44 (2): 432-435, 1974.
- ^ Boissonat, J.D .; A. Cerezo; K. Leblond (Mayıs 1992). "Düzlemde Sınırlı Eğriliğin En Kısa Yolları" (PDF). IEEE Uluslararası Robotik ve Otomasyon Konferansı Bildirileri. 3. Piscataway, NJ. sayfa 2315–2320. doi:10.1109 / ROBOT.1992.220117.
- ^ Anisi, David (Temmuz 2003). "Bir Kara Aracının Optimal Hareket Kontrolü". İsveç Araştırma Savunma Ajansı. I650-1942. Alıntı dergisi gerektirir
| günlük =(Yardım) - ^ Bui, X.N .; J.D. Boissonnat; P. Soueres; J.P. Laumond (Mayıs 1994). "Dubins Holonomik Olmayan Robot için En Kısa Yol Sentezi". IEEE Robotik ve Otomasyon Konferansı. 1. San Diego, CA. s. 2–7. doi:10.1109 / ROBOT.1994.351019.
- ^ Manyam, Satyanarayana; Sivakumar Rathinam (2016). "Dubins Gezici Satıcının Optimumunu Sıkıca Bağlamak Üzerine". Dinamik Sistemler, Ölçüm ve Kontrol Dergisi. 140 (7): 071013. arXiv:1506.08752. doi:10.1115/1.4039099.
- ^ Satyanarayana G. Manyam, Sivakumar Rathinam, David Casbeer, Eloy Garcia (2017). "En Kısa Dubins Yollarını Sıkıca Sınırlandırmak Bir Sıralı Noktalar İçinden Geçer". Journal of Intelligent & Robotic Systems. 88 (2–4): 495–511. doi:10.1007 / s10846-016-0459-4.CS1 bakimi: birden çok ad: yazarlar listesi (bağlantı)
Dış bağlantılar
- Dubins Eğrileri Planlama Algoritmalarından Steven M. LaValle








